Experiment is the step in the scientific method that arbitrates between competing models or hypotheses.^[1][2] Experimentation is also used to test existing theories or new hypotheses in order to support them or disprove them.^[3][4] An experiment or test can be carried out using the scientific method to answer a question or investigate a problem. First an observation is made. Then a question is asked, or a problem arises. Next, a hypothesis is formed. Then experiment is used to test that hypothesis. The results are analyzed, a conclusion is drawn, sometimes a theory is formed, and results are communicated through research papers.

A good experiment usually tests a hypothesis. However, an experiment may also test a question or test previous results.

• Replication of results is "a standard procedure in the validation of any scientific discovery." [4]
• "Science was long protected from fraud by a built-in safety mechanism: to be generally accepted, experiments must be repeatable by others." [5]

It is important that one knows all factors in an experiment. It is also important that the results are as accurate as possible. If an experiment is carefully conducted, the results usually either support or disprove the hypothesis. An experiment can never "prove" a hypothesis, it can only add support. However, one repeatable experiment that provides a counterexample can disprove a theory or hypothesis. An experiment must also control the possible confounding factors -- any factors that would mar the accuracy or repeatability of the experiment or the ability to interpret the results.

• "... the results of an experiment can never uniquely identify the explanation. They can only split the range of available models into two groups, those that are consistent with the results and those that aren't."^[5]

Experiments are not the only method that scientists use to test hypotheses. An experiment usually refers to observations in which conditions are artificially controlled and manipulated by the experimenter to eliminate extraneous factors, often in a scientific laboratory. Information about nature is also gathered and hypotheses tested in observational studies and field studies, which are observations of phenomena in a natural setting, without control by the experimenter.

[edit] Types of experiments

[edit] Controlled experiments

To demonstrate a cause and effect hypothesis, an experiment must often show that, for example, a phenomenon occurs after a certain treatment is given to a subject, and that the phenomenon does not occur in the absence of the treatment. (See Baconian method.)

Standard curve

A controlled experiment generally compares the results obtained from an experimental sample against a control sample, which is practically identical to the experimental sample except for the one aspect whose effect is being tested (the independent variable). A good example would be a drug trial. The sample or group receiving the drug would be the experimental one; and the one receiving the placebo would be the control one. In many laboratory experiments it is good practice to have several replicate samples for the test being performed and have both a positive control and a negative control. The results from replicate samples can often be averaged, or if one of the replicates is obviously inconsistent with the results from the other samples, it can be discarded as being the result of an experimental error (some step of the test procedure may have been mistakenly omitted for that sample). Most often, tests are done in duplicate or triplicate. A positive control is a procedure that is very similar to the actual experimental test but which is known from previous experience to give a positive result. A negative control is known to give a negative result. The positive control confirms that the basic conditions of the experiment were able to produce a positive result, even if none of the actual experimental samples produce a positive result. The negative control demonstrates the base-line result obtained when a test does not produce a measurable positive result; often the value of the negative control is treated as a "background" value to be subtracted from the test sample results. Sometimes the positive control takes the quadrant of a standard curve.

An example that is often used in teaching laboratories is a controlled protein assay. Students might be given a fluid sample containing an unknown (to the student) amount of protein. It is their job to correctly perform a controlled experiment in which they determine the concentration of protein in fluid sample (usually called the "unknown sample"). The teaching lab would be equipped with a protein standard solution with a known protein concentration. Students could make several positive control samples containing various dilutions of the protein standard. Negative control samples would contain all of the reagents for the protein assay but no protein. In this example, all samples are performed in duplicate. The assay is a colorimetric assay in which a spectrophotometer can measure the amount of protein in samples by detecting a colored complex formed by the interaction of protein molecules and molecules of an added dye. In the illustration, the results for the diluted test samples can be compared to the results of the standard curve (the blue line in the illustration) in order to determine an estimate of the amount of protein in the unknown sample.

Controlled experiments can be performed when it is difficult to exactly control all the conditions in an experiment. In this case, the experiment begins by creating two or more sample groups that are probabilistically equivalent, which means that measurements of traits should be similar among the groups and that the groups should respond in the same manner if given the same treatment. This equivalency is determined by statistical methods that take into account the amount of variation between individuals and the number of individuals in each group. In fields such as microbiology and chemistry, where there is very little variation between individuals and the group size is easily in the millions, these statistical methods are often bypassed and simply splitting a solution into equal parts is assumed to produce identical sample groups.

Once equivalent groups have been formed, the experimenter tries to treat them identically except for the one variable that he or she wishes to isolate. Human experimentation requires special safeguards against outside variables such as the placebo effect. Such experiments are generally double blind, meaning that neither the volunteer nor the researcher knows which individuals are in the control group or the experimental group until after all of the data have been collected. This ensures that any effects on the volunteer are due to the treatment itself and are not a response to the knowledge that he is being treated.

In human experiments, a subject (person) may be given a stimulus to which he or she should respond. The goal of the experiment is to measure the response to a given stimulus by a test method.

Original map by John Snow showing the clusters of cholera cases in the London epidemic of 1854

[edit] Natural experiments

A natural experiment is an observational study in which the assignment of treatments to subjects has been haphazard: That is, the assignment of treatments to subjects has not been made by experimenters (and certainly not by randomization). Natural experiments are most useful when there has been a clearly defined and large change in the treatment (or exposure) to a clearly defined subpopulation, so that changes in responses may be plausibly attributed to the change in treatments (or exposure). Natural experiments are considered for study designs whenever controlled experimentation is difficult, such as in epidemiology and economics.

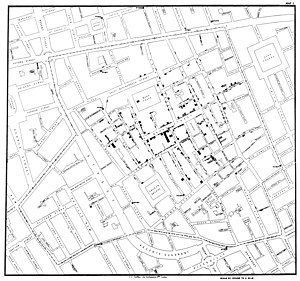
One of the most famous natural experiments was the 1854 Broad Street cholera outbreak in London, England. On 31 August 1854, a major outbreak of cholera struck Soho. Over the next three days 127 people near Broad Street died. By the end of the outbreak 616 people died. The physician John Snow identified the source of the outbreak as the nearest public water pump, which he identified using a map of deaths and illness. In this example, Snow discovered a strong association between the use of the water and deaths and illnesses due to cholera. Snow found that the water company (the Southwark and Vauxhall Company) that supplied water to districts with high attack rates obtained the water from the Thames downstream from where raw sewage was discharged into the river. By contrast, districts that were supplied water by the Lambeth Company, which obtained water upstream from the points of sewage discharge, had low attack rates. The water supply in mid-Nineteenth Century London wsa not developed by scientists studying cholera, and so exposure to this well may be considered a haphazard event. ^[6] Therefore, this exposure has been recognized as being a natural experiment. ^[7][8]

[edit] Field experiments

Field experiments are so named in order to draw a contrast with laboratory experiments. Often used in the social sciences, and especially in economic analyses of education and health interventions, field experiments have the advantage that outcomes are observed in a natural setting rather than in a contrived laboratory environment. However, like natural experiments, field experiments suffer from the possibility of contamination: experimental conditions can be controlled with more precision and certainty in the lab.

[edit] History

[edit] Francis Bacon

Francis Bacon was an English philosopher and scientist in the 1600s and an early and influential supporter of experimental science. He disagreed with the method of answering scientific questions by deduction and described it as follows: 'Having first determined the question according to his will, man then resorts to experience, and bending her to conformity with his placets, leads her about like a captive in a procession.'^[9] Bacon wanted a method that relied on repeatable observations, or experiments. He was notably the first to order the scientific method as we understand it today.

There remains simple experience; which, if taken as it comes, is called accident, if sought for, experiment. The true method of experience first lights the candle [hypothesis], and then by means of the candle shows the way [arranges and delimits the experiment]; commencing as it does with experience duly ordered and digested, not bungling or erratic, and from it deducing axioms [theories], and from established axioms again new experiments.

' Francis Bacon. Novum Organum. 1620.^[10]

When the problem or conditions do not permit a controlled experiment, such as in astronomical research, observational studies can be useful. For example, Tycho Brahe made careful observations and recorded measurements of stellar and planetary positions over time. After Brahe's death, his measurements proved useful in the development of Johannes Kepler's laws of planetary motion, which offered a better fit than did Ptolemy's theory.

In the centuries that followed, important advances and discoveries were made by people who applied the scientific method in different areas. For example, Galileo Galilei was able to accurately measure time and experiment to make accurate measurements and conclusions about the speed of a falling body. Antoine Lavoisier was a French chemist in the late 1700s who used experiment to describe new areas such as combustion and biochemistry and to develop the theory of conservation of mass (matter).^[11] During the 1800s, Louis Pasteur used the scientific method to disprove the prevailing theory of spontaneous generation and to develop the germ theory of disease.^[12] Because of the importance of controlling potentially confounding variables, the use of well-designed laboratory experiments is preferred when possible.

[edit] Galileo Galilei

Measured fall time of a small steel sphere falling from various heights. The data is in good agreement with the predicted fall time of , where h is the height and g is the acceleration of gravity.

Galileo Galilei (1564'1642) was a scientist who performed many quantitative experiments addressing many topics. Using several different methods, Galileo was able to accurately measure time. Previously, most scientists had used distance to describe falling bodies using geometry, which had been used and trusted since Euclid.^[13] Galileo himself used geometrical methods to express his results. Galileo's successes were aided by the development of a new mathematics as well as cleverly designed experiments and equipment. At that time, another kind of mathematics was being developed'algebra. Algebra allowed arithmetical calculations to become as sophisticated as geometric ones. Algebra also allowed the discoveries of scientists such as Galileo'as well as later scientists like Newton, Maxwell and Einstein'to be later summarized by mathematical equations. These equations described physical relationships in a precise, self-consistent manner.

One prominent example is the 'ball and ramp experiment.'^[14] In this experiment Galileo used an inclined plane and several steel balls of different weights. With this design, Galileo was able to slow down the falling motion and record, with reasonable accuracy, the times at which a steel ball passed certain markings on a beam.^[15] Galileo disproved Aristotle's assertion that weight affects the speed of an object's fall. According to Aristotle's Theory of Falling Bodies, the heavier steel ball would reach the ground before the lighter steel ball. Galileo's hypothesis was that the two balls would reach the ground at the same time.

Other than Galileo, not many people of his day were able to accurately measure short time periods, such as the fall time of an object. Galileo accurately measured these short periods of time by creating a pulsilogon. This was a machine created to measure time using a pendulum.^[16] The pendulum was synchronized to the human pulse. He used this to measure the time at which the weighted balls passed marks that he had made on the inclined plane. He measured to find that balls of different weights reached the bottom of the inclined plane at the same time and that the distance traveled was proportional to the square of the elapsed time.^[17] Later scientists summarized Galileo's results as The Equation of Falling Bodies.^[18][19]

Distance d traveled by an object falling for time t where g is gravitational acceleration (~ 9.8 m/s2):

These results supported Galileo's hypothesis that objects of different weights, when measured at the same point in their fall, fall at the same speed because they experience the same gravitational acceleration.

[edit] Antoine Lavoisier

Lavoisier and Laplace's ice calorimeter device

Antoine Lavoisier (1743'1794) was a French chemist regarded as the founder of modern chemistry. Lavoisier's experiments were among the first truly quantitative chemical experiments. He showed that, although matter changes its state in a chemical reaction, the quantity of matter is the same at the end as at the beginning of every chemical reaction.^{[citation needed]} In one experiment, he burned phosphorus and sulfur in air to see whether the results further supported his previous conclusion (Law of Conservation of Mass). In this experiment, however, he determined that the products weighed more than the original phosphorus and sulfur. He decided to do the experiment again. This time he measured the mass of the air surrounding the experiment as well. He discovered that the mass gained in the product was lost from the air. These experiments provided further support for his Law of Conservation of Mass.

One of Lavoisier's experiments connected the worlds of respiration (physiology) and combustion. Lavoisier's hypothesis was that combustion and respiration were one and the same, and combustion occurs with every instance of respiration. Lavoisier, working with Pierre-Simon Laplace, designed an ice calorimeter apparatus for measuring the amount of heat given off during combustion or respiration. This machine consisted of three concentric compartments. The center compartment held the source of heat, in this case, the guinea pig or piece of burning charcoal. The middle compartment held a specific amount of ice for the heat source to melt. The outside compartment contained packed snow for insulation. Lavoisier then measured the quantity of carbon dioxide and the quantity of heat produced by confining a live guinea pig in this apparatus. Lavoisier also measured the heat and carbon dioxide produced when burning a piece of charcoal in the calorimeter. Using this data, he concluded that respiration was in fact a slow combustion process. He also discovered through precise measurements that these processes produced carbon dioxide and heat with the same constant of proportionality. He found that for 224 grains of 'fixed air' (CO₂) produced, 13 oz. of ice was melted in the calorimeter. Converting grains to grams and using the energy required to melt 13 oz. of ice, one can compute that for each gram of CO₂ produced, about 2.02 kcal of energy was produced by the combustion of carbon or by respiration in Lavoisier's calorimeter experiments. This compares well with the modern published heat of combustion for carbon of 2.13 kcal/g.^[20] This continuous slow combustion, which Lavoisier and Laplace supposed took place in the lungs, enabled the living animal to maintain its body temperature above that of its surroundings, thus accounting for the puzzling phenomenon of animal heat.^[21] Lavoisier concluded, 'Lla respiration est donc une combustion," That is, respiratory gas exchange is combustion, like that of burning a candle.

Lavoisier was the first to conclude by experiment that the Law of Conservation of Mass applied to chemical change.^[22] His hypothesis was that the mass of the reactants would be the same as the mass of the products in a chemical reaction. He experimented on vinous fermentation (biochemistry). He determined the amounts of hydrogen, oxygen, and carbon in sugar. He weighed a quantity of sugar, added yeast and water in measured amounts, and allowed the mixture to ferment. Lavoisier measured the mass of the carbonic acid gas and water that were given off during fermentation and weighed the residual liquor, the components of which were then separated and analyzed to determine their elementary composition.^[23] In this way he controlled a couple of potential confounding factors. He was able to capture the carbonic acid gas and water vapor that were given off during fermentation so that his final measurements would be as accurate as possible. Lavoisier then concluded that the total mass of the reactants was equal to the mass of the final product and residue.^[24] Moreover, he showed that the total mass of each constituent element before and after the chemical change remained the same. Similarly, he demonstrated via experimentation that the mass of products of combustion is equal to the mass of the reacting ingredients.

[edit] Louis Pasteur

(Above) A swannecked flask is pictured with broth and no bacteria in it after being boiled to remove any germs or microorganisms. (Below) Another swannecked flask is pictured with outside contaminants in the air allowed in. This broth grows microorganisms.

Louis Pasteur (1822'1895), regarded as the 'Father of Microbiological sciences and immunology,' was a French biologist during the 1800s.^[25] He discovered and supported by experimental results the idea that disease-causing agents do not spontaneously appear but are alive and need the right environment to prosper and multiply. Stemming from this discovery, he used experiment to develop vaccines for chicken cholera, anthrax and rabies, and to develop methods for reducing bacteria in some food products by heating them (pasteurization). His work also led him to advocate (along with the English physician Dr. Joseph Lister) for antiseptic surgical techniques. Most scientists of that day believed that microscopic life sprang into existence from nonliving matter. This idea was called spontaneous generation.

Pasteur's observations of tiny organisms under the microscope caused him to doubt spontaneous generation. He designed an experiment to test it. His hypothesis was that life could not arise from where there is no life. He took care to control possible confounding factors. For example, he needed to make sure there was no life, even microscopic, in the flasks of broth he used as a test medium. He decided to kill any microscopic organisms already present by boiling the broth until he was confident that any microorganisms present were killed. Pasteur also needed to make sure that no microscopic organisms entered the broth after boiling, yet the broth needed exposure to air to properly test the theory. A colleague suggested a flask with a neck the shape of an 'S' turned sideways. Dust (which Pasteur thought contained microorganisms) would be trapped at the bottom of the first curve, but the air would flow freely through.^[26]

Thus, if bacteria should really be spontaneously generated, then they should be growing in the flask after a few days. If spontaneous generation did not occur, then the contents of the flasks would remain lifeless. In the end, it was a complete success; not a single microorganism appeared in the broth. Then Pasteur allowed the dust containing the microorganisms to mix with the broth. In just a few days the broth became cloudy from millions of organisms growing in it. For two more years, he repeated the experiment in various conditions and locales to assure himself that the results were correct. In this way Pasteur supported his hypothesis that spontaneous generation does not occur.^[27] Despite the experimental results supporting his hypotheses and his success curing or preventing various diseases, correcting the public misconception of spontaneous generation was a slow, difficult process.

As he worked to solve specific problems, Pasteur's notions were sometimes corrected by the results of his experiments, such as when he was asked to find the cause of disease devastating the French silkworm industry in 1865. After a year of diligent work he correctly identified a culprit organism and gave practical advice for developing a healthy population of moths. However, when he tested his own advice, he found disease still present. It turned out he had been correct but incomplete ' there were two organisms at work. It took two more years of experimenting to find the complete solution.^[28]

[edit] Observational science

Observational science is used when it is impractical to fit a system into a laboratory setting. It can also be used when confounding factors are either limited or known well enough to analyze the data in light of them. In order for an observational science to be valid, the confounding factors must be known and accounted for.

[edit] Astronomy

An early European observational scientist was Tycho Brahe (1546'1601). Brahe's observations of stellar and planetary positions were noteworthy both for their accuracy and quantity.^[29] His celestial positions were much more accurate than those of any predecessor or contemporary. In an observatory funded for him by King Frederick II of Denmark, Brahe built some of the largest observing instruments yet constructed.^[30] Because of the large size of this equipment, Brahe was able to measure angles to an accuracy of better than 0.1 degree.^[31] This was more accurate than any previous observations and close to the limit that the human eye can observe.^[31] In this way, Brahe was able to make observations about stellar and planetary positions in a lab setup.

Brahe himself was not a Copernican but proposed a system in which the Sun and Moon orbited the Earth, while the other planets orbited the Sun. His system provided a safe position for astronomers who were dissatisfied with older models but were reluctant to accept the Earth's motion. It gained a considerable following after 1616 when Rome decided officially that the heliocentric model was contrary to both philosophy and Scripture, and could be discussed only as a computational convenience that had no connection to fact. His system also offered a major innovation: while both the geocentric model and the heliocentric model as set forth by Copernicus relied on the idea of transparent rotating crystalline spheres to carry the planets in their orbits, Brahe eliminated the spheres entirely.

Johannes Kepler (1571'1630) used the accurate observations of Brahe to discover the shape of Mars' orbit. His first hypothesis was that the orbit was circular. After four years of research and testing 70 different combinations of circles and epicycles, he devised a shape that would fit Mars' orbit. However, the model was accurate to only 0.13 degrees.^[32] Kepler knew that Brahe's observations could be used to develop an orbit shape more accurate than this. Kepler eventually decided to try various oval shaped orbits. This implied that the speed of the planet changed as it traveled around the oval. After nine years, he found that elliptical orbits fit satisfactorily with the observed path of Mars. He found that this shape worked not only for Mars, but also for every planet that Brahe had observed.^[32]

[edit] Biology

Observational studies are not experiments. By definition, observational studies lack the manipulation required for Baconian experiments. In addition, observational studies in biological systems often involve variables that are challenges to quantify or control. Nevertheless, observational studies are used because it is sometimes too difficult (too expensive, or too much time required) or unethical to conduct longitudinal experiments with human or animal subjects. In these situations, observational studies have value because they often suggest hypotheses that can be tested with randomized experiments or by collecting fresh data.

In providing therapies for human subjects, for example in psychology or health care, it is unethical to provide a substandard treatment to patients. Therefore, ethical review boards are supposed to stop clinical trials and other experiments unless a new treatment is believed to offer benefits as good as current best practice.^[33] It is also unethical and often illegal to conduct randomized experiments on the effects of substandard or harmful treatments, such as the effects of ingesting arsenic on human health. To understand the effects of such exposures, scientists use observational studies.

Observational studies are limited because they lack the statistical properties of randomized experiments. In a randomized experiment, the method of randomization specified in the experimental protocol guides the statistical analysis, which is usually specified also by the experimental protocol.^[34] Without a statistical model that reflects an objective randomization, the statistical analysis relies on a subjective model.^[34] Inferences from subjective models are unreliable in theory and practice.^[35] In fact, there are several cases where carefully conducted observational studies consistently give wrong results, that is, where the results of the observational studies are inconsistent and also differ from the results of experiments. For example, epidemiological studies of colon cancer consistently show beneficial correlations with broccoli consumption, while experiments find no benefit.^[36]

A particular problem with observational studies involving human subjects is the great difficulty attaining fair comparisons between treatments (or exposures), because such studies are prone to selection bias, and groups receiving different treatments (exposures) may differ greatly according to their covariates (age, height, weight, medications, exercise, nutritional status, ethnicity, family medical history, etc.). In contrast, randomization implies that for each covariate, the mean for each group is expected to be the same. For any randomized trial, some variation from the mean is expected, of course, but the randomization ensures that the experimental groups have mean values that are close, due to the central limit theorem and Markov's inequality. With poor randomization, the systematic variation in covariates between the treatment groups (or exposure groups) makes it difficult to separate the effect of the treatment (exposure) from the effects of the other covariates, most of which have not been measured. The mathematical models used to analyze such data must consider each differing covariate (if measured), and the results will not be meaningful if a covariate is neither randomized nor included in the model.

To avoid these conditions that render an experiment far less useful, physicians conducting medical trials (such as for Food and Drug Administration approval), will quantify and randomize the covariates that can be identified. Researchers attempt to reduce the biases of observational studies with complicated statistical methods such as propensity score matching methods, which require large populations of subjects and extensive information on covariates. Outcomes are also quantified when possible (bone density, amount of some cell or substance in the blood, physical strength or endurance, etc.) and not based on a subject's or a professional observer's opinion. In this way, the design of an observational study can render the results more objective and therefore more convincing.

See also hierarchy of evidence and quasi-empirical methods.

[edit] See also

• Design of experiments
• Experimental physics
• Experimetrics
• List of experiments
• Long-term experiment
• True experiment

[edit] References

[edit] External links

• Lessons In Electric Circuits - Volume VI - Experiments
• Trochim, William M., Experimental Design, The Research Methods Knowledge Base, 2nd Edition. (version current as of July 11, 2006).
• Description of weird experiments (with film clips)
• Science Experiments for Kids
• Concept Development and Experimentation
• Shadish, William R., Thomas D. Cook, and Donald T. Campbell. 2002. Experimental and Quasi-experimental Designs for Generalized Causal Inference. Boston: Houghton Mifflin. 623 p.
• Guide for Understanding and Implementing Defense Experimentation (GUIDEx), The Technical Cooperation Program, 2006
• Experiment in Physics from Stanford Encyclopedia of Philosophy