This article needs additional citations for verification. Please help improve this article by adding reliable references. Unsourced material may be challenged and removed. (November 2010)

In electric circuit theory, an ideal voltage source is a circuit element where the voltage across it is independent of the current through it. A voltage source is the dual of a current source. In analysis, a voltage source supplies a constant DC or AC potential between its terminals for any current flow through it. Real-world sources of electrical energy, such as batteries, generators, or power systems, can be modelled for analysis purposes as a combination of an ideal voltage source and additional combinations of impedance elements.

A schematic diagram of an ideal voltage source, V, driving a resistor, R, and creating a current I

[edit] Ideal voltage sources

An ideal voltage source is a mathematical abstration that simplifies the analysis of electric circuits. If the voltage across an ideal voltage source can be specified independently of any other variable in a circuit, it is called an independent voltage source. Conversely, if the voltage across an ideal voltage source is determined by some other voltage or current in a circuit, it is called a dependent or controlled voltage source. A mathematical model of an amplifier will include dependant voltage sources whose magnitude is governed by some fixed relation to an input signal, for example.^[1] In the analysis of faults on electrical power systems, the whole network of interconnected sources and transmission lines can be usefully replaced by an ideal (AC) voltage source and a single equivalent impedance.

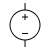Voltage Source	Current Source
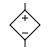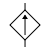Controlled Voltage Source	Controlled Current Source
Battery of cells	Single cell

Symbols used for voltage sources

The internal resistance of an ideal voltage source is zero; it is able to supply or absorb any amount of current. The current through an ideal voltage source is completely determined by the external circuit. When connected to an open circuit, there is zero current and thus zero power. When connected to a load resistance, the current through the source approaches infinity as the load resistance approaches zero (a short circuit). Thus, an ideal voltage source can supply unlimited power.

No real voltage source is ideal; all have a non-zero effective internal resistance, and none can supply unlimited current. However, the internal resistance of a real voltage source is effectively modeled in linear circuit analysis by combining a non-zero resistance in series with an ideal voltage source (a Thévenin equivalent circuit).

[edit] Comparison between voltage and current sources

Most sources of electrical energy (the mains, a battery) are modelled as voltage sources. An ideal voltage source provides no energy when it is loaded by an open circuit (i.e. an infinite impedance), but approaches infinite energy and current when the load resistance approaches zero (a short circuit). Such a theoretical device would have a zero ohm output impedance in series with the source. A real-world voltage source has a very low, but non-zero output impedance: often much less than 1 ohm.

Conversely, a current source provides a constant current, as long as the load connected to the source terminals has sufficiently low impedance. An ideal current source would provide no energy to a short circuit and approach infinite energy and voltage as the load resistance approaches infinity (an open circuit). An ideal current source has an infinite output impedance in parallel with the source. A real-world current source has a very high, but finite output impedance. In the case of transistor current sources, impedances of a few megohms (at low frequencies) are typical.

Since no ideal sources of either variety exist (all real-world examples have finite and non-zero source impedance), any current source can be considered as a voltage source with the same source impedance and vice versa. Voltage sources and current sources are sometimes said to be duals of each other and any non ideal source can be converted from one to the other by applying Norton's or Thevenin's theorems.

[edit] References and notes

1. ^ K. C. A. Smith, R. E. Alley , Electrical circuits: an introduction, Cambridge University Press, 1992 ISBN 0521377692, pp. 11-13

[edit] See also

• Bandgap voltage reference
• Current source
• Voltage divider
• Voltage regulator
• Voltage reference